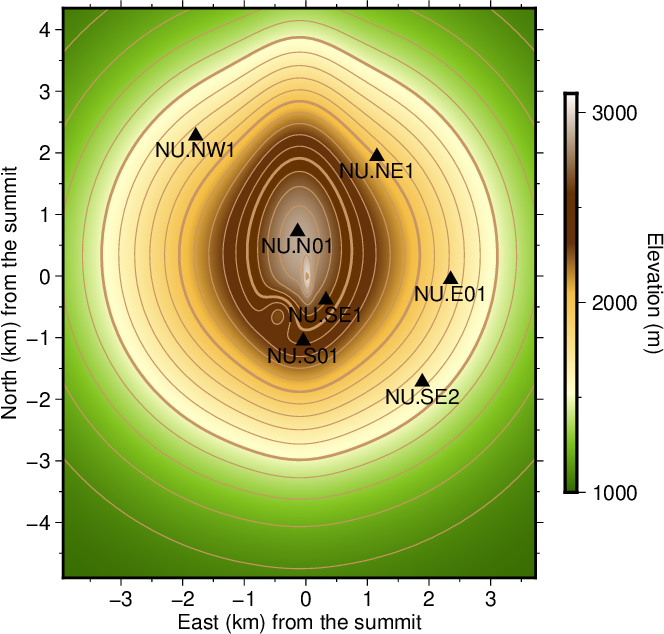
図2-1. 直交座標系による地形と観測点のプロット。
Fig. 2-1. A map of the topography and stations on a cartesian coordinate system.
|
sort -gr +2.0 -3.0 topography.dat | head |
|
34:22:40 137:12:34 2988.0 34:22:38 137:12:34 2988.0 34:22:38 137:12:36 2979.1 34:22:40 137:12:36 2978.6 34:22:42 137:12:34 2975.6 34:22:36 137:12:34 2972.7 34:22:42 137:12:36 2966.0 34:22:36 137:12:36 2964.3 34:22:44 137:12:34 2956.1 34:22:44 137:12:36 2946.3 |
|
latlon2xy --N=34.3840 --E=137.2080 --refN=34:22:39 --refE=137:12:34 |
| -132.8279 720.9692 |
|
awk '{ printf("%f\t%f\t%s\n",$2,$3,$1) }' stations_latlon.dat > tmp1.dat |
|
latlon2xy --inputfile=tmp1.dat --outputfile=tmp2.dat
--refN=34:22:39 --refE=137:12:34 |
|
awk '{ printf("%s\t%f\t%f\n",$3,$1,$2) }' tmp2.dat > stations_xy.dat |
|
latlon2xy --inputfile=topography.dat --outputfile=topography_xy.dat
--refN=34:22:39 --refE=137:12:34 |
|
#! /bin/bash -u # 横軸の設定 (Configuration of the lateral axis) xmin=`gmt info -C topography_xy.dat | awk '{ printf("%.2f",$1/1000.0) }'` xmax=`gmt info -C topography_xy.dat | awk '{ printf("%.2f",$2/1000.0) }'` xtics=1 mini_xtics=0.5 # 縦軸の設定 (Configuration of the vertical axis) ymin=`gmt info -C topography_xy.dat | awk '{ printf("%.2f",$3/1000.0) }'` ymax=`gmt info -C topography_xy.dat | awk '{ printf("%.2f",$4/1000.0) }'` ytics=1 mini_ytics=0.5 # 標高の設定 (Configuration of the elevation) zmin=1000.0 zmax=3100.0 zinc=1.0 ztics=1000.0 mini_ztics=500.0 # グラフのプロット位置とサイズの設定 (Configuration of the plotting location and size) x0=3.0 y0=3.0 width=8.0 height=`echo $width $xmin $xmax $ymin $ymax | awk '{ print $1*($5-$4)/($3-$2) }'` # カラーバーの設定 (Configuration of the color bar) colorbar_x=`echo $x0 $width | awk '{ print $1+$2+0.5 }'` colorbar_y=`echo $y0 $height | awk '{ print $1+$2/2.0 }'` colorbar_length=`echo $height | awk '{ print 0.7*$1 }'` # 出力ファイル名 (The output file name) outputfile_noExt=map_xy # プロットの開始 (Start plotting) gmt begin $outputfile_noExt ps # 座標軸の文字サイズを設定 (Set font size for coordinate axes) gmt set FONT_ANNOT_PRIMARY 10p # 地形データをgrdファイルに変換 (Convert the topography data to a grd format) awk '{ print $1/1000.0,$2/1000.0,$3 }' topography_xy.dat | gmt surface -R${xmin}/${xmax}/${ymin}/${ymax} -Gtopography_xy.grd -I0.01/0.01 # カラーパレットの作成 (Create a color pallete) gmt makecpt -Cdem1 -T${zmin}/${zmax}/${zinc} -Z # 地形を色で表現 (Plot the topography by colors) gmt grdimage topography_xy.grd -R${xmin}/${xmax}/${ymin}/${ymax} -JX${width}/${height} -Xa${x0} -Ya${y0} # カラーバーのプロット (Plot a colorbar) gmt colorbar -Dx${colorbar_x}/${colorbar_y}/${colorbar_length}/0.2 -Bxa${ztics}f${mini_ztics} # カラーバーのレジェンドのプロット (Plot a colorbar legend) echo ${colorbar_x} ${colorbar_y} | awk '{ print $1+1.4,$2,"Elevation (m)" }' | gmt text -R0/21/0/29.7 -JX21/29.7 -Xa0 -Ya0 -F+f10p+a270+jCB # 細い等高線(100 m間隔)をプロット (Plot thin topography contours at 100 m intervals) gmt grdcontour topography_xy.grd -R${xmin}/${xmax}/${ymin}/${ymax} -JX${width}/${height} -Xa${x0} -Ya${y0} -C100 -W0.4,200/150/100 # 太い等高線(500 m間隔)をプロット (Plot thick topography contours at 500 m intervals) gmt grdcontour topography_xy.grd -R${xmin}/${xmax}/${ymin}/${ymax} -JX${width}/${height} -Xa${x0} -Ya${y0} -C500 -W1.2,200/150/100 # 観測点位置を記号でプロット (Plot station locations by stations) awk '{ print $2/1000.0,$3/1000.0 }' stations_xy.dat | gmt plot -R${xmin}/${xmax}/${ymin}/${ymax} -JX${width}/${height} -Xa${x0} -Ya${y0} -St0.3 -G0/0/0 # 観測点コードをプロット (Plot station codes) awk '{ print $2/1000.0,$3/1000.0-0.1,$1 }' stations_xy.dat | gmt text -R${xmin}/${xmax}/${ymin}/${ymax} -JX${width}/${height} -Xa${x0} -Ya${y0} -F+f10p+jCT -Bxa${xtics}f${mini_xtics} -Bya${ytics}f${mini_ytics} -BWSen # 座標軸のレジェンドをプロット (Plot coordinate axis legends) xlabel_x=`echo $x0 $width | awk '{ print $1+$2/2.0 }'` xlabel_y=`echo $y0 | awk '{ print $1-0.6 }'` ylabel_x=`echo $x0 | awk '{ print $1-0.8 }'` ylabel_y=`echo $y0 $height | awk '{ print $1+$2/2.0 }'` gmt text -R0/21/0/29.7 -JX21/29.7 -Xa0 -Ya0 -F+f10p+a+j <<EOF $xlabel_x $xlabel_y 0 CT East (km) from the summit $ylabel_x $ylabel_y 90 CB North (km) from the summit EOF # プロットの終了 (Finish the plotting) gmt end # png形式に変換 (Convert to a png format) convert -trim -density 150 $outputfile_noExt.ps $outputfile_noExt.png |
 図2-1. 直交座標系による地形と観測点のプロット。 Fig. 2-1. A map of the topography and stations on a cartesian coordinate system. |